DMT Машина Тьюринга
| Добавил: | DMT | ||||||||||||||||||||||||||||||||||||||||||||||
| Дата создания: | 26 ноября 2007, 10:25 | ||||||||||||||||||||||||||||||||||||||||||||||
| Дата обновления: | 3 января 2008, 22:24 | ||||||||||||||||||||||||||||||||||||||||||||||
| Просмотров: | 34573 последний сегодня, 1:11 | ||||||||||||||||||||||||||||||||||||||||||||||
| Комментариев: | 3 | ||||||||||||||||||||||||||||||||||||||||||||||
|
Машиной
Тьюринга T = (A,Q,p ) называется тройка, состояний из непустых
конечных множеств A = {a0,a1,…,
an}, Q = {q0,q1,…,
qm} и частичной функции Здесь {L,S,R} – множество, состоящее из трех элементов. Оно одинаково для всех машин Тьюринга и интерпретируется командами перемещения головки: L – влево, R – вправо, S – стоять на месте. Множество А называется внешним алфавитом, его элементы – буквами. Буквы a0 и a1 для всех машин Тьюринга одинаковы: a0 = 0,a1 = 1. Элементы q0,…, qm называются внутренними состояниями. Частичная функция p называется программой и
записывается или с помощью прямоугольной таблицы, в которой в клетке (
qi,qj) записывается тройка · qiaj ® qkae означающей ( qk,ae,S) = p ( qi,aj), · qiaj ® qkaeR означающей ( qk,ae,R) = p ( qi,aj), · qiaj ® qkaeL означающей ( qk,ae,L) = p ( qi,aj). Эти команды обозначим через T( i,j). Машиным
словом , или конфигурацией, называется слово вида:
a
qkaeb , где Машинное слово: a qkaeb интерпретируется как положение, при котором головка указывает на символ ae, машина находится во внутреннем состоянии qk, слева от текущей ячейки находятся символы, составляющие слово a , а справа – слово b . В примере 1 машинное слово равно: 20qi931 для некоторого i. Пусть задана машина Тьюринга Т и машинное слово M = a qiajb , где 0 ? i ? m. Обозначим через MT’ слово, которое получается (за один такт) по правилам: 1) для i = 0 положим MT’ = M; 2) для i > 0 выполняем одно из следующих трех преобразований: · если T( i,j) = qiaj ® qkae, то MT’ = a qkaeb ; · в случае T( i,j) = qiaj® qkaeR, если b не пусто, то MT’ = a qk aeb , иначе MT ’= a qk ae a0; · в случае T( i,j) = qiaj ® qkaeL, если a = a 1 as для некоторых a 1 и as , то MT’ = a 1 qkas aeb , иначе (т.е. если a пусто) MT’= qka0aeb (дополнительная инструкция). Положим: MT0 = M, MT(n+1) = (MT( n))’. Будем говорить, что машина Т перерабатывает машинное слово М в слово М1, если MT( n) = M1 для некоторого n ? 0. Пишем: М ? T M1, если Т перерабатывает М в М1, и при этом не используется дополнительная инструкция (из правил образования слова MT’). Говорим, что машина Т вычисляет частичную функцию f: Nn ® N, если выполнены следующие условия: · если (x1,…, xn) I Dom( f), то машина Т останавливается, т.е. перерабатывает слово q101x10…1xn0 в некоторое слово a q0b , и при этом a q0b содержит f(x1,…, xn) вхождений символа 1 (здесь символы x1, … , xn обозначены через x 1, ..., xn ) ; ·
если (x1,…,
xn) не принадлежит Dom( f), то машина, начиная
со слова Говорим, что машина Т правильно вычисляет частичную функцию f: Nn ® N, если выполнены условия: · если (x1,…, xn) I Dom( f), то q101x10…1xn0 ? T q001f(x1,…, xn)0…0; · в противном случае машина, начиная со слова q101x10…1xn0, работает бесконечно. Частичная функция f называется (правильно) вычислимой, если существует машина Тьюринга, которая (правильно) вычисляет f. Пример 1Пусть машина Тьюринга T = {A, Q, p }, A = {0,1}, Q = {q0,q1,q2} задана с помощью таблицы:
Рассмотрим слово: M = q1011…10. На первом шаге выполняется команда q10® q20R. Получаем: MT’ = 0q211…10. Затем, до тех пор, пока слово не превратится в слово 011…1q20, будет выполняться команда q21 ® q21R. После этого будет выполнена команда q20 ® q01, и машина остановится, ибо q0 соответствует состоянию остановки. Входное слово, состоящее из x единиц, означает, что аргументом вычисляемой функции является число x. Поскольку на выходе получается x + 1 подряд идущих единиц, то машина вычисляет функцию: s( x) = x + 1. Пример 2Вычисление функции: s( x) = x+1 в примере 2 не является правильным. Построим машину Тьюринга для правильного вычисления:
Программа реализующая Машину Тьюринга - MashinTuring Работа с программой MashinTuring Программу Машины Тьюринга необходимо записать в виде таблицы команд: aKq, где: a - новое содержание текущей ячейки на ленте (0 или 1). K - команда лентопротяжного механизма машины Тьюринга (влево – 'L', вправо – 'R', стоп – 'S') q - новое внутренне состояние машины Тьюринга (' Q'+целое число от 0 до n) Для изменения содержимого ячейки информационной ленты необходимо щелкнуть правой кнопкой мыши (0) или левой (1) Главное окно программы:
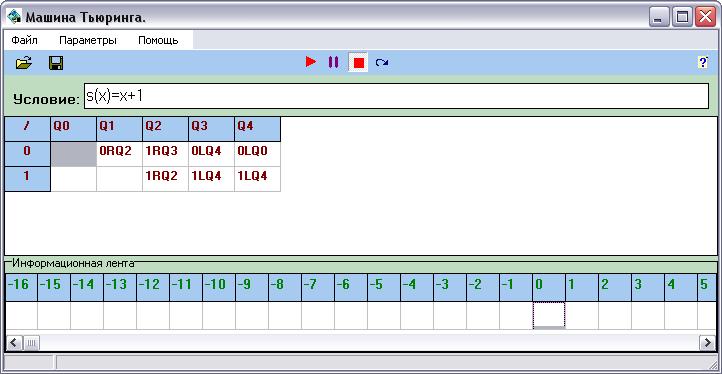 Данная программа воспроизводит все действия используя таблицу переходов,
состояний и ленту.
Регистрирует собственное расширение для своих
файлов. Данную программу запрещено размещать на сайтах и домашних страницах!!! Разрешено указавать следующую ссылку на программу:DMT Mashin Turing Разрешено передавать программу из "рук в руки" без публикации. Разрешено размещать программу в локальных сетях не имеющих доступа в Интернет. DMT ©
| |||||||||||||||||||||||||||||||||||||||||||||||
Комментарии для "DMT Машина Тьюринга"
|
Пользователь: lilo Сообщений: 38 Статус: Незримый Зарегистрирован: 8 января 2008, 12:39 Был:9 апреля 2008, 19:55   | Дата: 10 января 2008, 21:29 Сообщение № 1 |
| гдеж была эта программа, когда я лабы сдавала =)) |
|
Пользователь: kukusya Сообщений: 1 Статус: Незримый Зарегистрирован: 23 сентября 2008, 4:01 Был:24 сентября 2008, 2:26   | Дата: 23 сентября 2008, 4:03 Сообщение № 2 |
| ДА что тут скачевать!!!!!!!! тут же елы палы нет кода проги самой....а екзешка никому не надо!!!!! |
|
Пользователь: DMT Сообщений: 123 Статус: Программист Зарегистрирован: 18 октября 2007, 2:35 Был:13 ноября 2017, 4:54   | Дата: 23 сентября 2008, 11:51 Сообщение № 3 |
|
тут же елы палы нет кода проги самой Данная программа находится в разделе "Программы от DMTSoft" а не в разделе "Исходники" если Вы не заметили!!! Программа разработана для проверки правильности таблицы переходов и исходный код её никто выкладывать не хотел!!! незачем! А нужна она кому-нибудь или нет - решать к сожелению не Вам! Сделаете что-нибудь стоющее, нужно всем и выкладывайте - глядишь плюсик себе и заработаете, легче станет, пользу принесёт! Ваш комментарий изменён - вырезано нецензурное выражение. Оставьте его себе!!! |

 Выход
Выход